Un segnale sinusoidale è espresso della relazione :

A(t)= A sen

dove :

A (t) - Valore istanntaneo del segnale ( ampiezza )

A - Valore Massimo

= 2 f

f - Frequenza

Sfasamento Iniziale

 La frequenza f esprime il numero di oscillazioni complete in un secondo.Il periodo T invece è l’ intervallo di tempo corrispondente ad una oscillazione completa del segnale ed è legato alla frequenza dalla relazione :

Si dimostra che un segnale periodico di periodo T e di forma qualsiasi può essere rappresentato come somma di n segnali sinusoidali (armoniche), ciscuno caratterizzato da una terna di valori An,fn,, (Fig.04) con fn multiplo interno della frequenza f = 1/T, detta fondamentale:

fn = = n/T

Questi segnali componenti, compresi tra una frequenza minima ed una massima,costituiscono lo spettro di frequenza del segnale, cioè la sua banda (fig. 05).Nel corso degli anni per la trasmissione di informazione a distanza si è cercato di utilizzare una porzione di spettro sempre più estesa.

Fig. 04 Scomposizione in Armoniche di un segnale Periodico

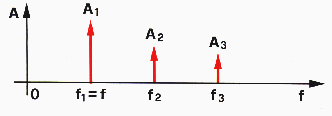
Fig. 05 Spettro di frequenza di un segnale Periodico

Nei sistemi di telecomunicazioni elettriche la trasmissione avviene sovrapponendo il segnale che contiene l’ informazione utile ad un’ onda elettromagnetica di elevata frequenza, ad un’ onda portante; cioè il segnale utile modula il segnale portante,che quindi viene trasmesso; a distanza è sufficente riconoscere l’ informazione trasportata dal segnale portante e trattarla come si desidera.Si aumenta la frequenza delle portanti aumenta la banda del segnale utile trasmissibile, fornendo quindi una maggiore capacità di trasmissione.Per tali ragioni la tendenza dello sviluppo dei sistemi di comunicazioni elettriche è stata quella di impiegare frequenze sempre più alte, corrispondenti a lunghezza d’ onda sempre più corte.