SIMMETRIA ASSIALE
Nella geometria piana la simmetria assiale, detta anche ribaltamento, e' una particolare rotazione di 180° intorno ad una retta detta asse di simmetria.
|
|
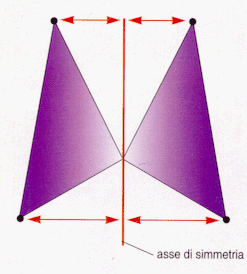
Due punti A e B si definiscono simmetrici rispetto alla retta r quando tale retta e' asse del segmento che li unisce, cioe' quando una retta r e' perpendicolare al segmento AB nel suo punto medio.
|
|
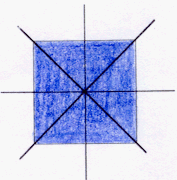
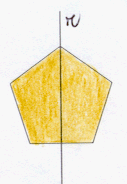
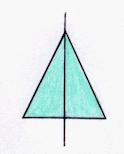
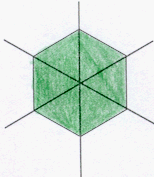
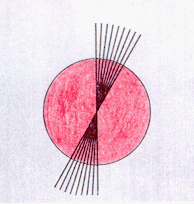
Una figura e' simmetrica rispetto ad un asse quando ogni suo punto ammette un simmetrico nella figura rispetto a quell' asse. |
|
Esempi di figure geometriche che ammettono assi di simmetria:
|
|
|
|
|
|
|
Il quadrato ha 4 assi di simmetria.
|
Il pentagono ed il triangolo isoscele hanno solo un asse di simmetria. |
L'esagono ha 3 assi di simmetria. |
Il cerchio ha infiniti assi di simmetria: i diametri. |
|
Se una figura ha due assi di simmetria perpendicolari fra loro, essa è simmetrica anche rispetto al punto di intersezione dei due assi (centro di simmetria).
Esempi : il quadrato e il rombo.
